定量分析数据的处理和评价
(一)分析结果的误差
误差是指测定值与真值之差。但是,由于分析方法的不完善,分析仪器精度的限制,分析环境温度、湿度的变化,分析人员的技术水平、经验等主客观因素,使分析结果不可避免地存在误差。即是说,误差自始至终存在于一切分析测定和分析的过程中,分析结果都有误差。如果对误差产牛的原因没有正确的认识,盲目地相信分析结果,有时会做出错误的结论,有时叉会对分析结果的正确性产生怀疑、犹豫,不敢报出数据,贻误生产、科研开发以及事故处理的正常进行。反之,如果分析工作者清楚地了解误差的属性及其产生的原因,就能通过对大量的原始分析数据进行科学的处理,得出符合客观实际的正确结论。因此,正确地认识分析数据的误差、分析数据的处理方法和评价是分析工作者必须正视的问题。
误差按其性质以及对测定值可靠性的影响而言,可以分为三类;随机误差、系统误差和过失误差。
(二)随机误差、标准偏差和精密度
1随机误差
随机误差是分析过程中系列因素微小的随机作用而形成的具有相互抵偿性的误差,它是不可避免且无法校准的误差。在一次测定中,随机误差的大小无法预言,没有任何规律性。但在多次测定中,随机误差出现还是有规律的,具有统计规律性。随着测定次数的增加,正、负误差相互抵偿,误差平均值趋于零。因此,在日常分析中,不能用一次的泓定值作为最终结果报出,需要进行多次的测定,让其误差平均值趋于零,然后求出多次平行测定结果的平均值,方可作为最终的结果。
随机误差决定分析结果的精密度。随机误差大,分析结果的精密度差,反之亦然。随机误差一般用偏差来表示。所谓偏差是指测
定值与测定平均值之差,一般有如下表示方式。
绝对偏差d:

标准偏差σ(简称标准差)

当测定次数为有限次时,标准偏差可用
S表示
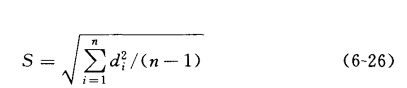
相对标准偏差RSD(又称变异系数cv):

平时用得最多的是标准偏差。它是偏差的统计平均值,叉称均方根偏差,是表示整个测定值离散度的特征值。
标准偏差的特点是对一组测量值中的极值(即误差大的数值)反应比较灵敏,比较明显反映出测定值的波动情况,准确地反映出平行测定结果的好坏,用它来衡量分析结果的精密度。也就是说,若标准偏差(S)大,说明存在偶然误差,例如人为因素、仪器不稳或环境波动等因素都会造成大的标准偏差。
那么,误差范围是多少才算是合理的、可以接受的呢’这就是所谓2σ(或3σ)原则。从误差理论可知,随机误差是正态分布,其理论概率密度函数φ(x)为
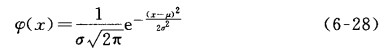
式中μ- 被测量值的真值;
σ——标准偏差;
x..单次测定值。
当用标准偏差a作为衡量测定值的误差尺度时,可以根据上式计算具有各种大小误差的测岳值出现的概率。出现偏差大于2倍标准偏差的概率为5%,大于3倍标准偏差的测量值只有0. 3%,是小概率事件。而通常的分析测试中,只进行不多的几次测定,出现大偏差测定值的概率是非常小的。一旦出现这样大偏差的测量值,有理由怀疑它不是随机误差造成的,很可能存在系统误差或者别的原因。所以在有限的分析测试中,可以用样本标准偏差S代替总体标准偏差一。当每次测定的偏差S大干2a(或3一)时,即说明存在偶然误差,此数据可“考虑剔除掉。
增加平行测定的次数能够提高分析结果的精度,可是增加测定次数很快会遇到麻烦,稍微提高一点精度就需要付出很大代价,消耗很多精力和时间。表6-7是平均标准偏差SI与测定次数的关系。

从表中可以看出,平行测定2-4次即可;当分析结果要求较高时,可测定5 -9次就足够了,不要为追求好的结果而盲目地增加测定次数。
2精密度
精密度是指在相同条件下,对同一量进行多次重复测定时测定值的离散程度,测定值越集中,测定精密度越好。有的资料也称为测定的重复性,所以精密度又可以说是用测定数据的重复性来表示误差的大小。
表征精密度好坏是前面所讨论的式(6-24) -式(6-27)各式,其中最常用的是标准偏差。若存在偶然误差,标准偏差变大,分析结果的精密度变差。要提高分析精密,必须力戒避免偶然误差。而好的精密度是保证获得良好准确度的先决条件。精密度同被测物的浓度大小有关。测定常量物质比测定痕量物质的精密度高,标准偏差小。因此在报告测定值精密度时,应该指明获得该精密度的被测物的浓度范围。
总而言之,分析结果精密度的好坏是获得准确分析结果的前提,差的精密度说明分析过程中存在偶然误差,这种偶然误差通常用标准偏差束表示。
(三)系统误差和准确度
l系统误差
系统误差是指在一定的试验条件下,由某个或某些因素按照某,确定的规律起作用而形成的误差。系统误差的符号及其大小是不变的或在试验条件改变时按照某一确定的规律变化。增加测定次数·不能发现和减小系统误差,只有改变试验条件才能发现系统误差。系统误差产生的原因是没和校正的。在气体色谱分析中系统误差的主要来源如下。
①色谱仪的硬件设计不台理,如分流器构造不合理,放大器衰减不成比例;信号响应不在线性范围等因素引起。
②定量分析数据处理不当,如采用不正确的校正曲线、校正因子或者标准气不纯而造戒。
③由于个人的习惯与偏向,如在读取进样器、移液管、读数放大器刻度时读数偏向一方,引起数据偏高或偏低而引起的误差。
④由于数据处理系统参数设定不合理,基线判断错误而引起。
系统误差决定测定结果的准确度。当系统误差存在时,会使测定值与真值之间产生偏倚,偏倚的大小以误差或相对误差表示。
绝对误差(简称误差)E:
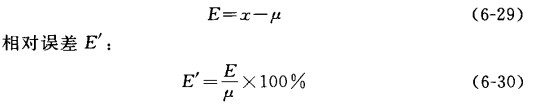
式中各符号同前。
用得最多是相对误差,它是表示误差在真值中所占的比例。它不仪能反映误差大小,而且能反映测定的准确度,相对误差愈小,表示测定的准确度愈高。
那么,怎样才能知道分析测定中是否存在系统误差呢’由于系统误差决定准确度的大小。因此确定系统中是否存在系统误差往往跟估计和确定准确度大小是联系在一起的,只是一个问题从不同的角度去叙述而已。在实际工作中,通常用标准物质或标准方法进行比对实验来确定、估计系统误差或准确度的存在及其大小。如果测得标准物质的量值在~定置信度下与标准物质的标准值一致,说明分析方法和测定过程不存在系统误差,测量值是可靠的(而准确度是可相信的)。反之,如果测得标准物质的量值在一定置信度下与标准物质的标准值不一致,表明存在系统误差,造成准确度下降。这种系统误差可能来自分析方法或(和)测定过程。当找不到基体,量值与被恻样品相匹配的标准物质(如底气不同的标准气)时,则用标准方法进行比对实验,而这种标准方法一定是公认的、可溯源的标准分析方法。比较两种方法的测定值以判定在用分析方法的测定值是否存在系统误差,如果结果是一致的,说明无系统误差,准确度可靠,否则就是存在系统误差,准确度必须进行校正。
另外,用加标回收率来评估准确度,也是分析人员普遍采用的一种方法。一般认为,只要回收率落在指定的范围内,如回收率为95% ~105%,测量值就不存在系统误差。其实这种认识是一种误区,也是很多分析人员容易犯的错误。因为存在的系统误差可以是固定系统误差,在一组测定中每一个测定量值都增大或减少一十同样的量;也可以是相对系统误差,测定误差与被测组分的量值成比例,在每个测定量值中引入一个固定百分误差。如果存在的是固定系统误差,测定误差不随被测物的质量而改变,按加标计算回收率是1OO%左右,只能说明加标的量值范围不存在系统误差,但不能排除固定系统误差隐含在加标前的测定量值中的可能性。如果存在相对系统误差,加标量测定受到干扰,产生一个固定百分比的误差,反映在加标回收率上,回收率自然是1oo%。因此,用加标回收率(%)来评定测量值的准确度,只适用于检查有无相对系统误差,而不能发现测定量值中的固定系统误差。在分析测试中,通常用回归分析来判断有无固定系统误差或相对系统误差。
取几份不等量的试样进行测定,然后对其进行回归分析,建立相应的回归方程,求出回归系数6(斜率)和常数n(截距)。其中n表示与被测组分浓度无关的周定系统误差,如果a=0.校正曲线通过原点,无固定系统误差,如果a显著地区别于。,则表明存在固定系统误差。而回归系数6,即校正曲线的斜率表示与浓度有关的因素,如果b =l,不存在相对系统误差,如果b显著地区别于1.则存在相对系统误差。因此,在进行加标回收率试验以确定是否存在系统误差时,最好先做回归分析,在证实不存在相对系统误差后,方可做加标回收率试验。
2准确度
准确度表示在-定条件下,试样的梗4定值与真值之间的符合程度,也就是测量值与真值之差大小的量值。由于气相色谱定量是相对法定量,真值是不知道的,所以无法计算定量的准确度。但是,正如前面所述,测定误差遵守正态分布,在一组测定数据中平均值是出现概率最大的值,单个测定值对平均值的偏差之和为零,偏差平方和最小,是真实值的无偏估计值。因此,在实际工作中,将几次测定值的平均值作为真值的估计值使用。表6-8和表6-9为工业气相色谱分析中允许的相对误差范围。
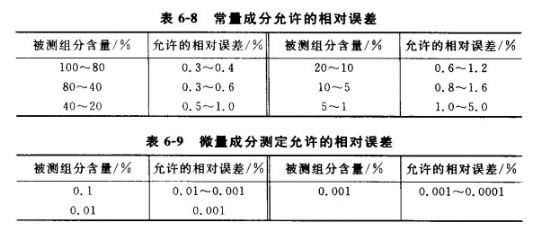
简而言之,系统误差是某些因素按照某一确定的规律起作用而形成的误差,使测量产生偏倚。这种误差可以校正,它影响定量的准确度,常用相对误差表示。
(四)过失误差
过失误差是分析测定人员粗枝大叶、操作不当而产生的数值远大于正常情况下的随机误差和系统误差。这种误差无规律可循,显然是与事实不符的误差,其实质则是测定过失。
我们说,测定误差是不可避免的,是指随机误差是不可避免的,系统误差是可以避免的,过失误差是不允许也是不应该发生的。

